DFN from a graph approach
Graph-based flow modeling approach adapted to multiscale discrete-fracture-network models
Context
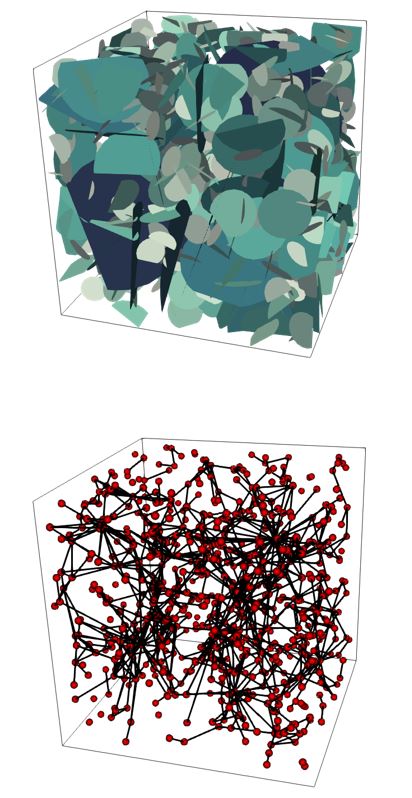
In crystalline rocks, fracture networks form the main pathways for flow. It is thus tempting to model flow and transport with the Discrete Fracture Network (DFN) approach, which aims at incorporating the complex multiscale fracture network structure. Topology (i.e., how elements relate to each other) is a critical property of any DFN, which is well represented by graphs. There is a growing interest in using graphs to infer a quantitative estimate of the flow and transport properties (permeability, transport times and channeling). Graphs preserve the topology of the DFN, even complex ones, and they are simple enough to allow flow and transport calculations to be solved quickly.
Project Results
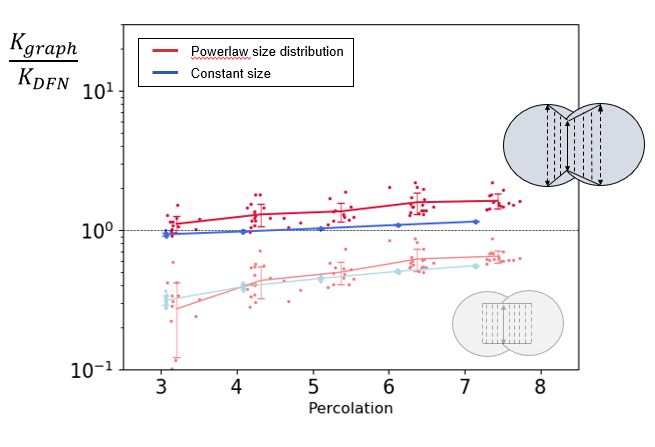
The graph type (vertices representing fractures or intersections) and the conductance of graph edges (links) are both important elements to consider for a reliable estimate of flow. First, we derive analytically a new expression of the edge conductance that preserves the fracture flow properties. The particularities in this expression are the use of the fracture size and the consideration of the fracture degree (number of intersections with other fractures). Second, we compare the graph predictions in terms of flow with direct DFN simulations. Different DFN topologies are tested (densities, fracture size distributions). We show that the method provides a reliable estimation of the DFN flow properties without requiring any later adjustment.
Find out more
Doolaeghe, D., Davy, P., Hyman, J. D., & Darcel, C. (2020). Graph-based flow modeling approach adapted to multiscale discrete-fracture-network models. Physical review E, 102(5), 053312.